prufer序列

prufer序列是一个比较实用的东西，一切与度数有关的树上计数问题，都可以用它以及它的性质来解决。

转化1：从无根树到prufer序列

现在，给你一棵树，我们要考虑如何把它变成prefur序列。
我们需要重复进行以下操作，直至树中只剩下两个点：

• 找到一个度数为 1，且编号最小的点。（其中编号最小保证了后面将会提到的prufer序列的唯一对应性，同时也方便从 prufer 序列转化回无根树）
• 把这个点的父亲节点加入序列，然后把这个点从树中删除。然后我们就得到了一个长度为 n − 2 的序列，这就是prufer序列。

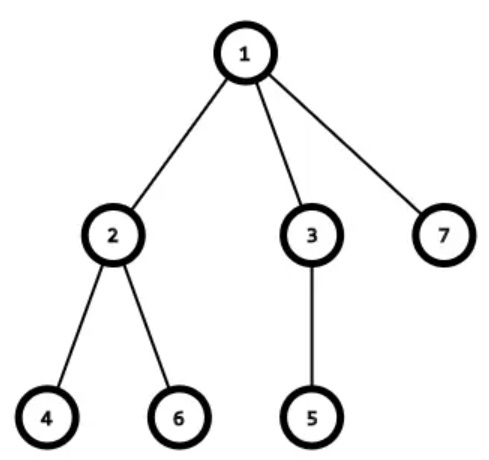
以上面的图为例，我们可以模拟这一过程如下：

• 找到4号节点，将其父结点加入序列，然后将其删去。此时序列：{2}。
• 找到5号节点，将其父结点加入序列，然后将其删去。此时序列：{2,3}。
• 找到3号节点，将其父结点加入序列，然后将其删去。此时序列：{2,3,1}。
• 找到6号节点，将其父结点加入序列，然后将其删去。此时序列：{2,3,1,2}。
• 找到2号节点，将其父结点加入序列，然后将其删去。此时序列：{2,3,1,2,1}。
  所以，最后得到的prufer序列就是{2,3,1,2,1}。

代码实现：

void prufer_code() {
    for(int i = 1; i <= n; i ++) cin >> f[i], d[f[i]] ++;
    for(int i = 1, j = 1; i <= n - 2; i ++, j ++) {
        while(d[j]) j ++;
        p[i] = f[j];
        while(i <= n - 2 && !--d[p[i]] && p[i] < j) p[i + 1] = f[p[i]], i ++;
    }
}

转化2：从prufer序列到无根树

还是以刚才那棵树为例，我们要考虑如何把它的prefur序列变回它本身。

我们需要重复进行以下操作，直至点集中只剩下两个点：（初始化所有点都在点集中）

• 取出prufer序列最前面的元素x。
• 取出在点集中的、且当前不在prufer序列中的最小元素y。（这恰好呼应了前面提到过的选取编号最小的节点）
• 在x,y之间连接一条边。（注意前面的取出相当于删除）
  最后，我们在点集中剩下的两个点中连一条边。
  显然这有n−1条边，且绝对不会形成环，因此它是一棵树，且就是原树。

以上面的序列为例，我们可以模拟这一过程如下：

• 取出2,4连边。此时prufer序列：{3,1,2,1}，点集：{1,2,3,5,6,7}。
• 取出3,5连边。此时prufer序列：{1,2,1}，点集：{1,2,3,6,7}。
• 取出1,3连边。此时prufer序列：{2,1}，点集：{1,2,6,7}。
• 取出2,6连边。此时prufer序列：{1}，点集：{1,2,7}。
• 取出1,2连边。此时prufer序列：{}，点集：{1,7}。

最后再在1,7间连边，就可以得到原树了。

代码实现：

void prufer_decode() {
    for(int i = 1; i <= n - 2; i ++) cin >> p[i], d[p[i]] ++;
    p[n - 1] = n;
    for(int i = 1, j = 1; i < n; i ++, j ++) {
        while(d[j]) j ++;
        f[j] = p[i];
        while(i < n && !--d[p[i]] && p[i] < j) f[p[i]] = p[i + 1], i ++;
    }
}

prufer序列的性质及相关结论